Graph

A graph is a non-linear data structure that consists of a collection of vertices (nodes).

Terminology

• Vertex or node that holds the data and it can have one ore more adjecent vertices
• Edge is the connection between two nodes
• Neighbor the neighbor of a node are the nodes that connected with it by edge
• Degree the number of edges that connected with vertex

Directed vs Undirected

Undirected Graphs

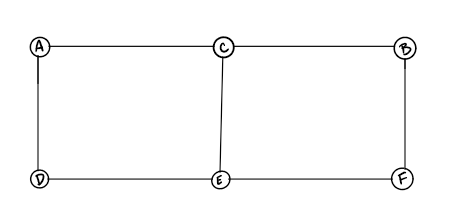
An Undirected Graph is a graph where each edge is undirected or bi-directional. This means that the undirected graph does not move in any direction.

Example -> friendship on Facebook, if *a* is friend of *b* then *b* is also friend of *a*

Directed Graphs

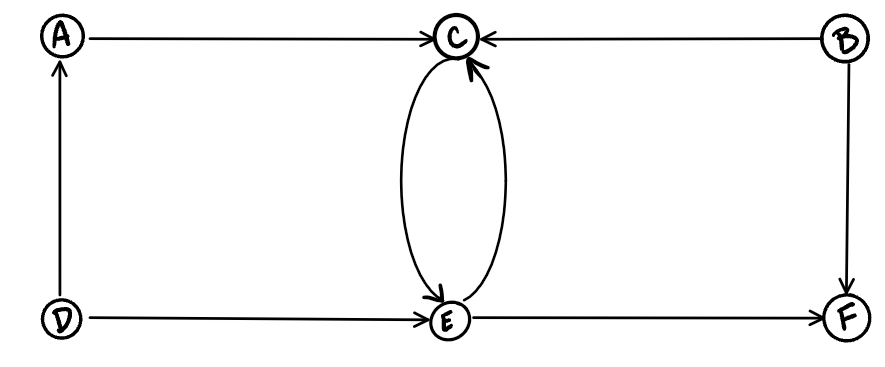
A Directed Graph also called a Digraph is a graph where every edge is directed.

Unlike an undirected graph, a Digraph has direction. Each node is directed at another node with a specific requirement of what node should be referenced next.

Example -> followers on Twitter, if *a* follows *b* then *b* not necessarily follows *a*

Complete vs Connected vs Disconnected

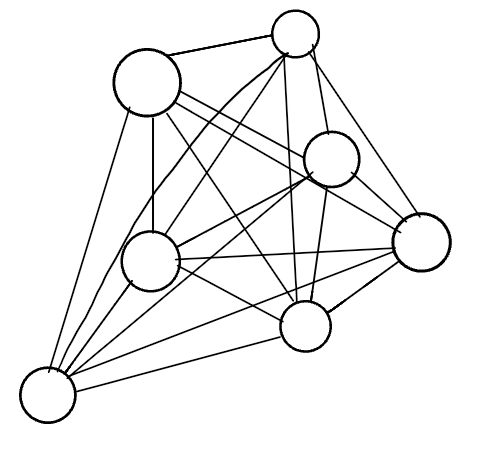
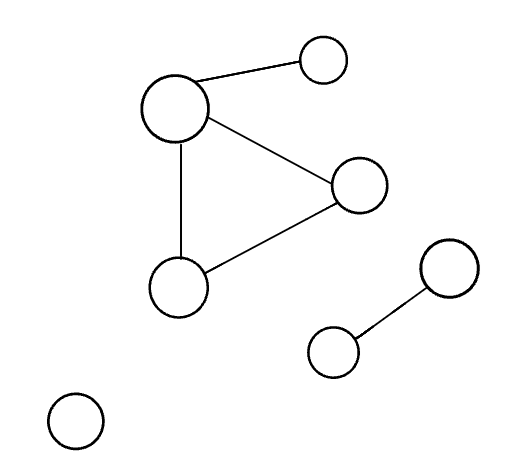
Complete Graphs

when each vertex connected to all vertices in the graph. As shown in the image below:

Connected Graphs

when each vertex has at least on connection with another vertex. As shown in the image below:

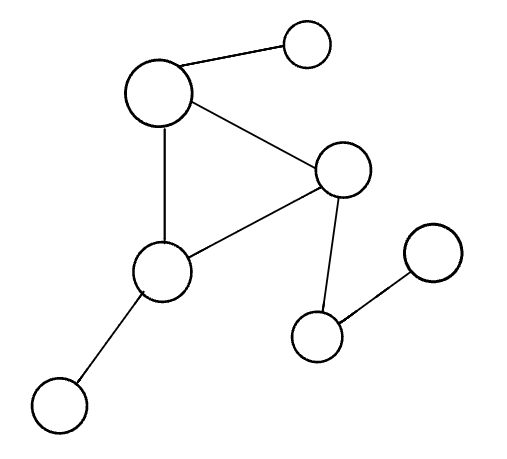
Disconnected Graphs

when some of the vertices is not connected with others(they have no edges). As shown in the image below:

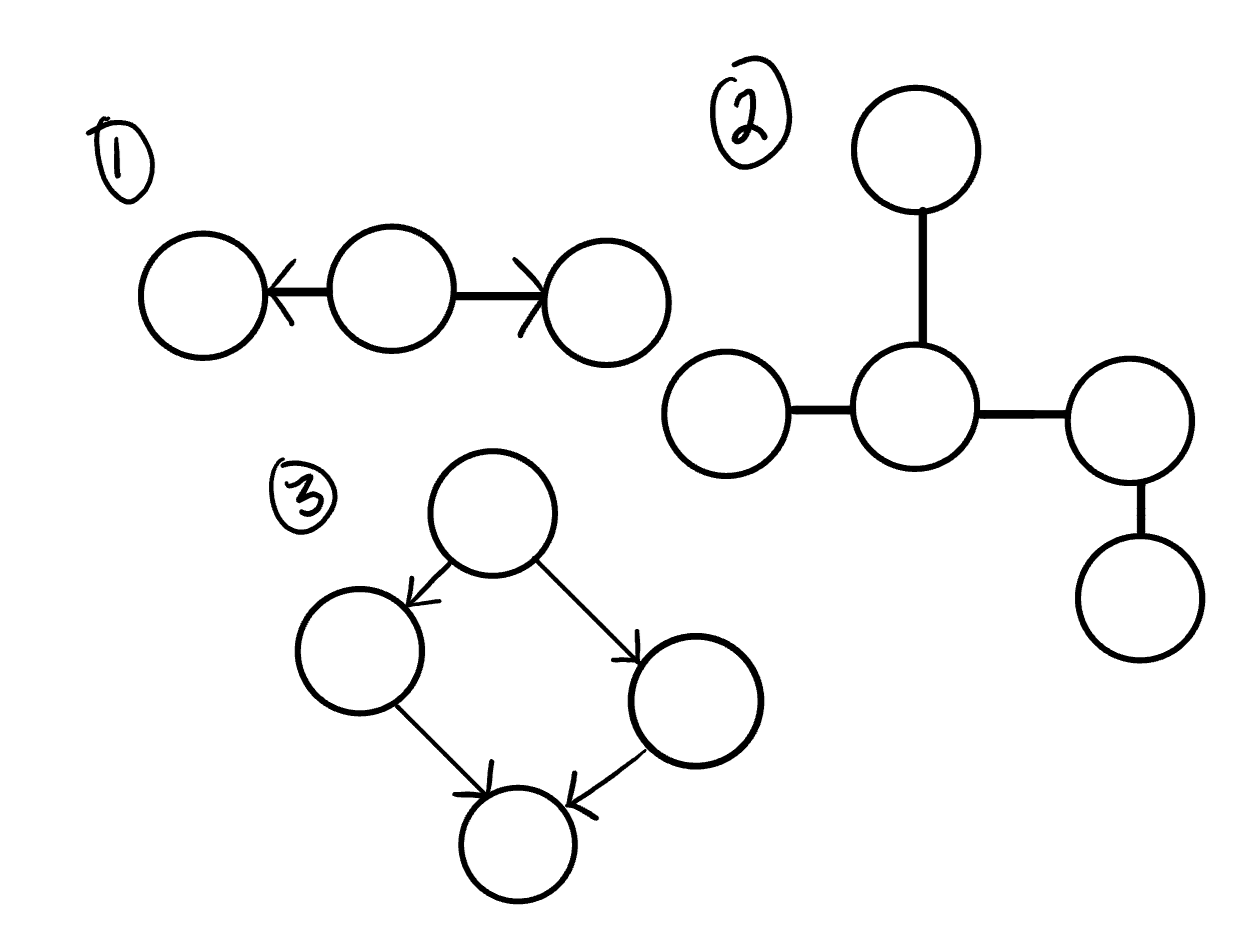
Acyclic vs Cyclic

Acyclic Graphs

An acyclic graph is a directed graph without cycles.

A cycle is when a node can be traversed through and potentially end up back at itself.

A directed acyclic graph is also called a DAG. This can also be represented as what we know as a tree.

As shown in the image below:

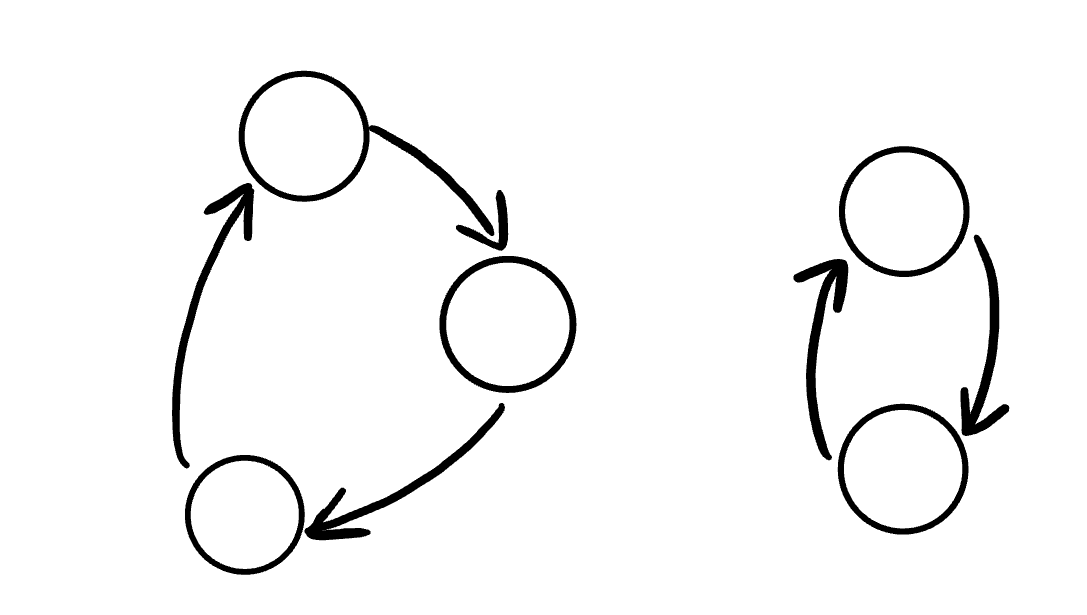
Cyclic Graphs

A Cyclic graph is a graph that has cycles.

A cycle is defined as a path of a positive length that starts and ends at the same vertex.

As shown in the image below:

Graph Representation

There are two ways to represent a graph:

1. Adjacency Matrix
2. Adjacency List

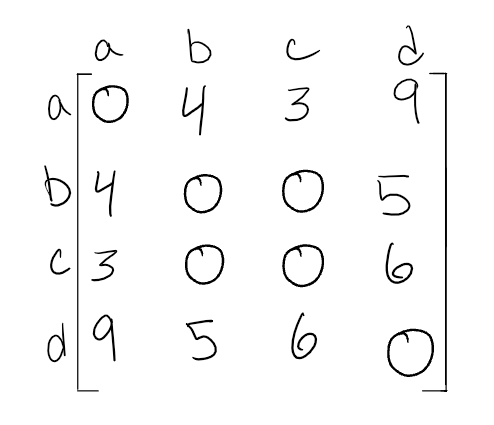
Adjacency Matrix

2-D array created to represent a graph, each row and column represnts each vertex.

if the node connected with another node 1 is being added, and 0 for no connection between the two nodes.

sparse graph is when there are very few connections.

dense graph is when there are many connections

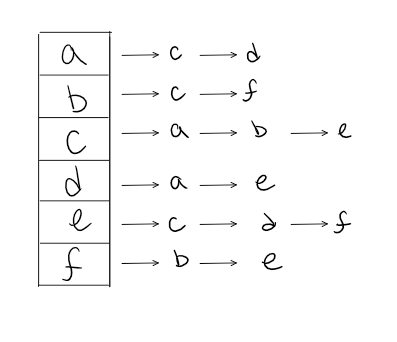
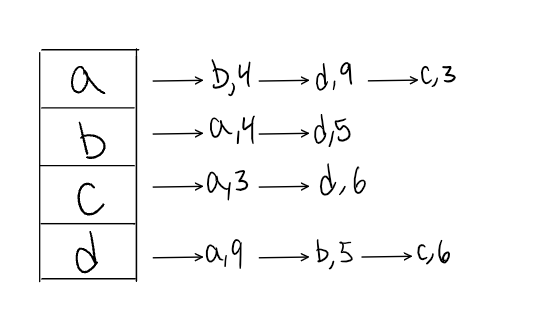
Adjacency List

An adjacency list is the most common way to represent graphs.

An adjacency list is a collection of linked lists or array that lists all of the other vertices that are connected.

Adjacency lists make it easy to view if one vertices connects to another.

Weighted Graphs

A weighted graph is a graph with numbers assigned to its edges. These numbers are called weights

When representing a weighted graph in a matrix, you set the element in the 2D array to represent the actual weight between the two paths. If there is not a connection between the two vertices, you can put a 0, although it is known for some people to put the infinity sign instead.

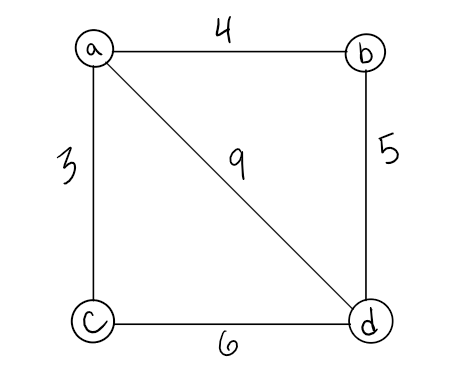
Within adjacency lists, you must include both the weight and the name of the adjacent vertex.

Traversals

Breadth First Traversal BFT

• it uses queue and set to keep track of visited nodes
• if the graph has islands, they won’t be visited

Depth First Traversal DFT

• it uses stack and set to keep track of visited nodes
• if the graph has islands, they won’t be visited

Real World Uses of Graphs

Graphs are extremely popular when it comes to it’s uses. Here are just a few examples of graphs in use:

1. GPS and Mapping
2. Driving Directions
3. Social Networks
4. Airline Traffic
5. Netflix uses graphs for suggestions of products